逻辑回归是二分类任务中最常用的机器学习算法之一。它的设计思路简单,易于实现,可以用作性能基准,且在很多任务中都表现良好。
本文从以下几个方面讲述逻辑回归:
- 什么是逻辑回归?
- 它是如何工作的。
- 逻辑回归 vs 线性回归
- 优缺点
- 何时适用
- 多分类任务(OvA, OvO)
- 其他分类算法
- 总结
什么是逻辑回归
和很多其他机器学习算法一样,逻辑回归也是从统计学中借鉴过来的,尽管名字里有回归两个字,但它不是一个需要预测连续结果的回归算法。与之相反,逻辑回归是二分类任务的首选方法。它输出一个0到1之间的离散尔值结果。简单来讲,它的结果不是0就是。
癌症检测算法可看做是逻辑回归问题的一个简单例子,这种算法输入病理图片并且应该辨别患者患有癌症(1)或没有癌症(0)。
它是如何工作的?
逻辑回归通过使用其固有的逻辑函数估计概率,来衡量因变量(目标预测标签)与一个或者多个自变量(特征)之间的关系。
然后这些概率必须二值化才能真的进行预测。这就是逻辑函数的任务,也称为sigmoid函数。sigmoid函数是一个S形曲线,它可以将任意实数值映射到介于0和1之间的值,但不能取0或1.然后使用阈值分类器将0和1之间的值转换为0或1.
下图说明了逻辑回归得出预测所需的所有步骤。
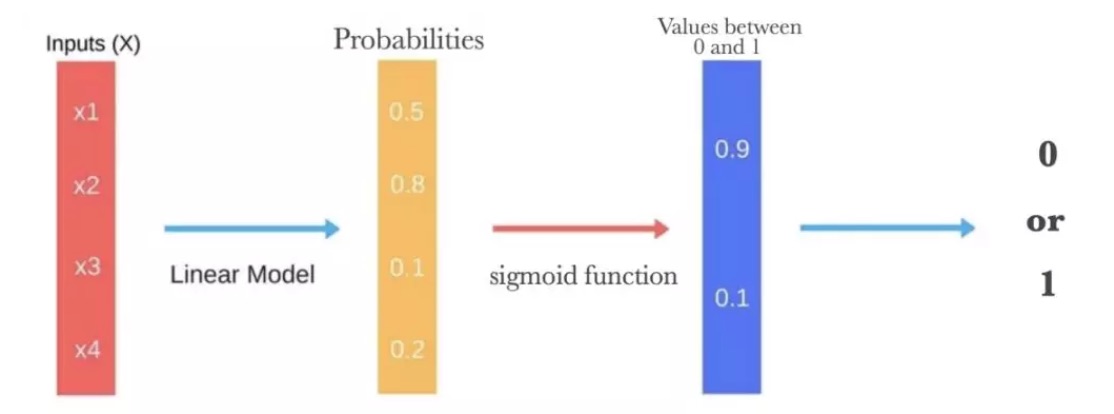
假设函数 (Hypothesis function)
逻辑回归的假设函数形式如下:

这个函数称为sigmoid函数,也称为逻辑函数,其函数曲线如下:
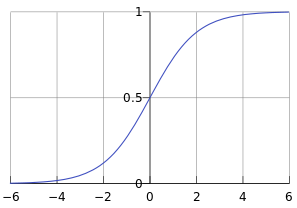
从上图可以看到sigmoid函数是一个s形的曲线,它的取值在[0,1]之间,在远离0的地方函数的值会很快接近0/1.这个性质使我们能够以概率的方式来解释。
一个机器学习的模型,实际上就是把决策函数限定在某一组条件下,这组限定条件就决定了模型的假设空间。当然,我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是:
这里的g(h)是上面提到的sigmoid函数,相应的决策函数是:
选择0.5作为阈值是一个一般的做法,实际应用时特定情况可以选择不同阈值。
决策边界(Decision Boundary)
决策边界,也称为决策面,是用于在N维空间,将不同类别样本分开的平面或曲面。
线性决策边界:
决策边界: -3 + x1 +x2 = 0
非线性决策边界
决策边界: -1 + x1^2 +x2^2 = 0
决策边界其实是一个方程,在逻辑回归中,决策边界由theta’ X=0定义。 假设函数(h=g(z))用于计算样本属于某种类别的可能性;决策函数(h=1(g(z)>0.5))用于计算样本的类别;决策边界(θ^Tx=0)是一个方程,用于标识出分类函数(模型)的分类边界。
代价函数(Cost Function)
逻辑回归中,采用如下的形式计算样本的代价值:
整合一下,得到逻辑回归中的代价函数:
优化方法
在逻辑回归中,使用梯度下降法对代价函数进行优化,完整形式如下:
注意: 逻辑回归和线性回归问题中,梯度下降算法的形式看上去一致,但实际上两者完全不同,因为假设函数是不同的,需要特别注意这一点。
其向量化实现(vectorized implementation)如下:
逻辑回归 vs 线性回归
逻辑回归得到一个离散的结果,线性回归得到一个连续的结果。预测房价的模型返回连续结果,是线性回归。癌症检测的结果是你有癌症或没有,是逻辑回归。
优缺点
逻辑回归是一种被人们广泛使用的算法,它非常高效,不需要太大的计算量,又通俗易懂,不需要缩放输入特征,不需要任何调整,且容易调整,并且输出校准好的预测概率。与线性回归一样,当你去掉和输出变量无关的属性以及相似度高的属性时,逻辑回归效果确实会更好。因此特征处理在逻辑回归和线性回归的性能方面起着重要的作用。
逻辑回归的另一个优点是它非常容易实现,且训练起来很高效。 它的一个缺点就是我们不能用逻辑回归来解决非线性问题,因为它的决策边界是线性的。
何时适用
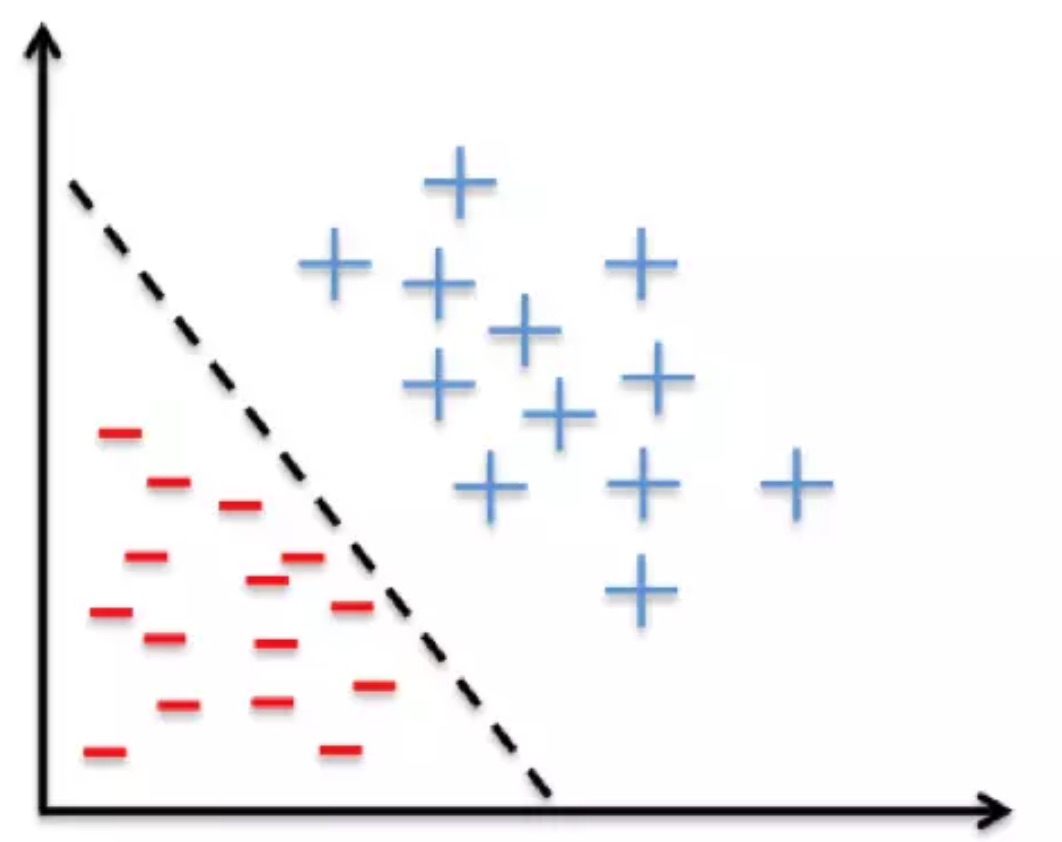
逻辑回归通过线性边界将你的输入分成两个区域,每个类别划分一个区域。因为,你的数据应当是线性可分的,如下图: