本文是 https://ml.berkeley.edu/blog/posts/vq-vae/ 一文的翻译。
就像机器学习社群的所有人一样,我们对OpenAI发布的DALL-E的生成结果感到不可思议。这个模型可以根据文本信息生成精确的,高质量的图像。该模型可以渲染出一些在现实世界不存在的问题,比如“牛油果形状的扶手椅”。
为了庆祝DALL-E的发布,我们准备写一个系列文章去解释DALL-E模型的关键部分。
该系列博客的第一篇会来介绍VQ-VAE,VQ-VAE是DALL-E的一部分,它使得该模型可以生成如此多种多样的高质量的图像。
在下一篇博客里面我们将会介绍用于多模态,自回归的模型transformers。transformers是DALL-E的另外一部分,它主要用来学习语言和图像之间的相关性,有了语言和图像之间的相关性,DALL-E才能产生如此有创意且准确的输出。
Note: 这篇博客需要读者了解一些深度学习和贝叶斯概率的知识。
基础
VQ-VAE 是 Vector Quantized Variational Autoencoder 的缩写,这里面有很多的大词,因此,让我们先简要回顾一下基础知识。
我们首先定义隐空间(latent space)的概念,然后再定义自编码器(autoencoder),最后,在解读 VQ-VAE 之前,我们将回顾变分自编码器的基础知识(Note: 如果你对这部分知识很熟悉,请直接跳开这部分,直接去到解读VQ-VAE细节的部分)
隐空间(Latent Space)
隐空间是对给定的原始数据分布的一些潜在的“隐藏”表示。让我们看一些例子来更清楚的理解这个概念。
想象一下原始数据是 x ∈ R_n, 它们是通过线性变换从某个较低维度 z ∈ R_m 生成的(m < n).具体来说,x 是通过 x =Az + v 来生成的,其中 v 是 n 维独立同分布高斯噪声,A ∈ R_nxm.
一般来说,我们只会看到原始数据x;我们无法访问z,这也是为什么它会被称为数据的潜在或“隐藏”表示。不过,我们想要获得z,因为它是一个更基本的,压缩的数据表示。此外,对于需要使用该数据的算法,这种隐示的数据表示可以成为更为有用的输入。
原始数据是隐空间的一种线性转换的这个设定,和无监督经典算法PCA的定义很像。PCA本质上试图从上面的例子中找到底层的z表示。PCA很棒,但如果潜在表示和原始数据之间有着更复杂的非线性关系呢?举例来说,下图显示了更复杂的隐空间能编码出高层次的信息。在这个例子中,PCA 将无法找到最佳的潜在表示。 相反,我们可以使用自动编码器来找到这个更抽象的潜在空间。
Note: 隐空间不需要是连续的向量空间,它可以是一组离散的变量,这也是VQ-VAE的隐空间类型。但在我们开始之前,让我们先了解一下自编码器。

自编码器(Autoencoders)
自编码器属于无监督学习方法,它使用神经网络为给定的数据寻找非线性的潜在表示。神经网络分成两个部分:一个编码器,z=f(x),一个解码器 x’ = g(z).
x 是输入数据,z是隐向量,x’是 x从隐空间中的重建。f(x) 和 g(z) 同为神经网络。把两个放在一起,整个模型可以被描述为 x’ = g(f(x))(看下图)
理想情况下,解码器应该能够从编码器的隐表示中准确的重建出原始数据。如果模型能够学习出这种重建,那我们就可以假设我们的隐空间可以很好的代表了原始数据。为了实现这一目标,我们训练一个模型,其中在x和x’之间加入重建loss.

同样需要注意的是,z的维度应该始终低于x。毕竟,自编码器的重点是找到原始目标数据的压缩空间,这样,算法就被迫找到原始数据中最重要的部分。
自编码器的这个压缩,潜伏的部分通常被称为网络的瓶颈部分,因为它将数据挤压到一个更小的空间里。
变分自编码器(Variational Autoencoders VAE)
Note: 本文不会详细介绍VAE的数学细节,想了解VAE更多的数学细节,可以阅读这篇blog:https://jaan.io/what-is-variational-autoencoder-vae-tutorial/
现在我们了解了自编码器的基本原理,让我们看看什么事变分自编码器,他有什么不同。VAE的关键区别是隐空间的结构,理想情况下,我们希望隐空间将语义相似的数据点放在一起,并将语义不同的点放置得很远。且最好是大部分的数据分布应该在潜空间中构成一个相当紧凑的体积,而不是延伸到无限大。
自编码器的主要问题是得到的隐空间不具备上述的两个属性.模型可以学习任何它想要的潜在空间,所以它经常通过将个别数据点放在自己的隐空间的远处来记忆它们。
下图直观地展示了自动编码器隐空间的这些问题,并将其与VAEs进行比较。

变分自编码器通过在隐空间上执行概率先验来克服这个问题。为了形式化这一点,将我们的隐空间z视为一个随机变量。首先让我们对隐向量执行一个先验p(z),在多数VAEs中这个先验是一个N(0,1)的高斯分布。给定一组原始数据x,我们还定义了隐空间的后验为p(z|x)。
我们的目标是是计算数据的后验p(z|x),我们可以使用贝叶斯规则。不过由于我们处理的是连续变量,所以p(x)是一个难以计算的量。为了让p(x)能够被计算,我们将后验近似为一个特定的分布:独立高斯。称之为q(z|x)。现在我们的目标变成最小化真实后验和近似之间的KL散度。

这里省略数学细节,最小化的目标可以通过最小化损失函数来计算。
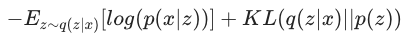
这里q(z|x)代表编码器的近似表示, p(x|z) 是解码器的表示
VAE 的 loss 看起来很直观,第一部分是重建损失,第二部分是后验的正则化。后验被KL散度拉向先验,基本上将隐空间调整为高斯先验。这就把隐空间数据紧凑的分布在了在0附近。
在神经网络能力足够的情况下,VAE 隐可以非常巧妙地拟合复杂的数据分布。通常情况下,我们可以看到在隐空间中不同类型数据点之间有着平滑的过度。例如,一个在MNIST上训练得到的VAE模型,隐空间中预期会有一个6的集群,和一个5的集群。如果我们在两个数据簇之间移动,我们会看到一个看起来数字5和6混合的奇怪数字。
基础小结
- 隐空间是数据的一种压缩,通常是数据的最重要和语义上最有趣的特征。
- 学习到的隐向量对许多下游算法都有用
- 自编码器是一种寻找隐空间的方法,这些隐空间是数据的复杂非线性函数。
- 变分自编码器会在自编码器的隐空间上加一个先验。这可以帮助学习到的隐空间拥有一些非常好的属性(即我们可以通过隐空间平滑地插入数据)
离散空间
接下来介绍什么是 VQ-VAE。VAE和VQ_VAE的最基础的不同点是VAE学习的是一个连续的隐表示,而VQ-VAE学习的是一个离散的表示。
我们知道如何使用连续连续的向量空间来表示自编码器的隐信息。不过隐信息不需要非得是连续的向量,他其实只需要能对目标数据进行一些数字表示。一个可能的理想方案是,用离散表示来代替向量空间。
一般来说,现实世界中遇到的很多数据都倾向于离散表示。例如,人类语音是由离散的音素和语言来表示的。此外,图像包含一些离散的限定词集的离散对象。你可以想象有一个离散变量代表物体的类型,一个代表它的颜色,一个代表它的尺寸,一个代表它的方向,一个代表它的形状,一个代表它的纹理,一个代表背景颜色,一个代表背景纹理,等等。
除了离散表示之外,还有很多算法(如transformer)用来处理离散数据,因此我们希望为这些算法使用离散的数据表示。

显然离散的隐表示很有用,但应该如何学习这样的表示呢? 一开始看起来这个任务非常有挑战,因为,离散数据在深度学习中表现不佳。 幸运的是,VQ-VAE 只需对 vanilla 自编码器范例进行一些调整,就使得深度学习在该任务中工作了。
量化自编码器
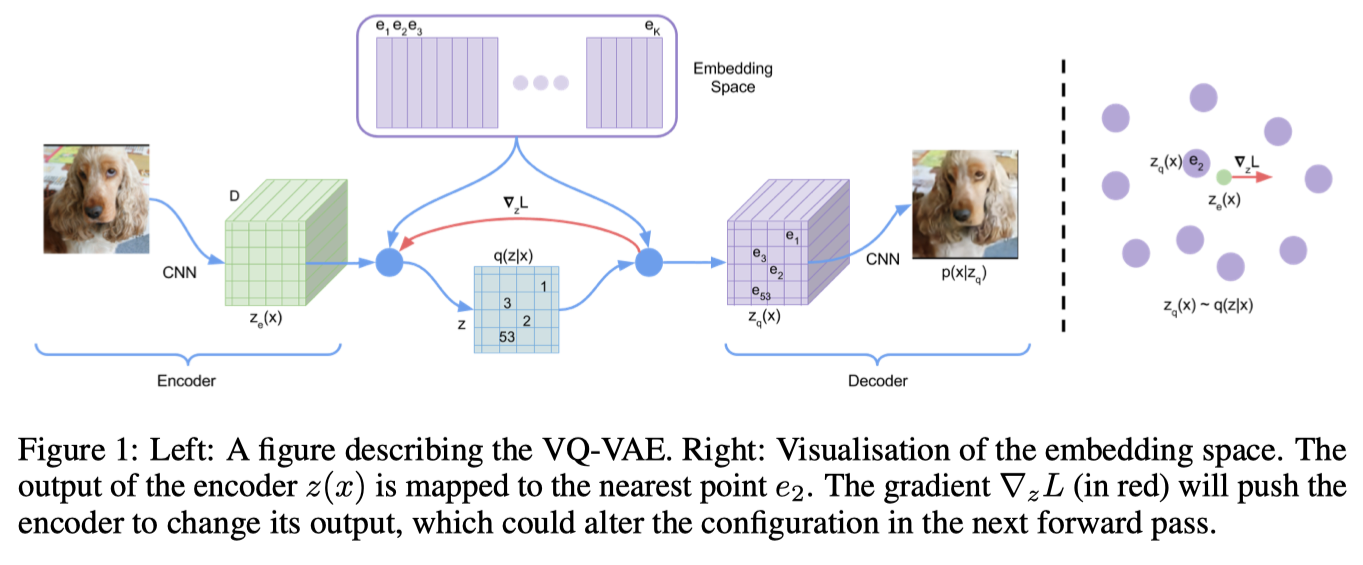
VQ-VAE在VAE的基础上向网络中添加了一个离散的codebook。cookbook是一组索引相关的向量列表。它被用来量化VAE的bottleneck部分;编码器网络的输出和codebook中的所有向量进行比较,把欧氏距离上最接近codebook的向量送入编码器。
数学表达是:z_q(x) = argmin_i||z_e(x) - e_i ||2,z_e(x)是输入x的编码向量,e_i是第 i 个 codebook向量,z_q(x)是量化向量,当作解码器的输入。
这个 argmin 操作对于编码器是不可微的。但实际上,如果把编码器梯度直接传递给编码器,就可以正常完成网络训练过程中的梯度回传工作。(即把和编码器相关的量化codebook向量梯度设置为1,其余的codebook向量梯度设置为0)。
解码器的任务是根据标准VAE公式,利用量化向量的输入完成重建。

生成多个代码
我们可能对仅仅使用如此有限的一组codebook向量是否能够有足够的表达能力。当解码器只能接受一组codebook向量作为输入时,怎么能够期望模型能够生成大量,具备多样性的图像?我们需要每个训练点的唯一离散值才能重建所有数据。那么模型会不会是通过记住每个训练点对应的离散codebook?
如果编码器只输出一个向量,上述的问题会有可能出现,但在实际使用VQ-VAE的过程中,编码器通常会产生一系列向量。例如,对于图像,编码器可能会输出一个32x32的向量网格,每个向量都被量化,然后整个网格被送入编码器。或者类似的,为了处理音频,编码器可以输出一长串一维向量。所有向量都被量化为相同的codebook,因此离散值的数量不会改变,但是通过输出多个code,我们能够以指数方式增加我们的解码器可以构建的数据点的数量。
举一个例子,想象我们处理的数据是图像,定一个长度是512的codebook,编码器的输出是一个32x32的网络。这种情况下,解码器可以输出2^9216个不同的图像。
学习 codebook
和编码器,解码器一样,codebook也是通过梯度下降的方式学习到的。理想情况下,