什么是StableDiffusion
stable diffusion是在 High-Resolution Image Synthesis with Latent Diffusion Models 这篇论文的基础上研究而成的。
Latent diffusion:
- 基于扩散模型的图像生成领域发展迅速,扩散模型生成的图像真实度高,质量好。但是基于像素空间的扩散模型对GPU资源的要求非常高。
training the most powerful DMs often takes hundreds of GPU days (e.g. 150 1000 V100 days in and repeated evaluations on a noisy version of the input space render also inference expensive, so that producing 50k samples takes approximately 5 days on a single A100 GPU.
- Latent diffusion 模型提出在latent space做diffusion的过程,latent space相较pixel space,在大小上有了很大的压缩(latent diffusion中,从512x512x3 压缩到 64x64xk)
- 设计了一种基于cross-attention的通用条件生成控制机制,能够实现多模态的训练。
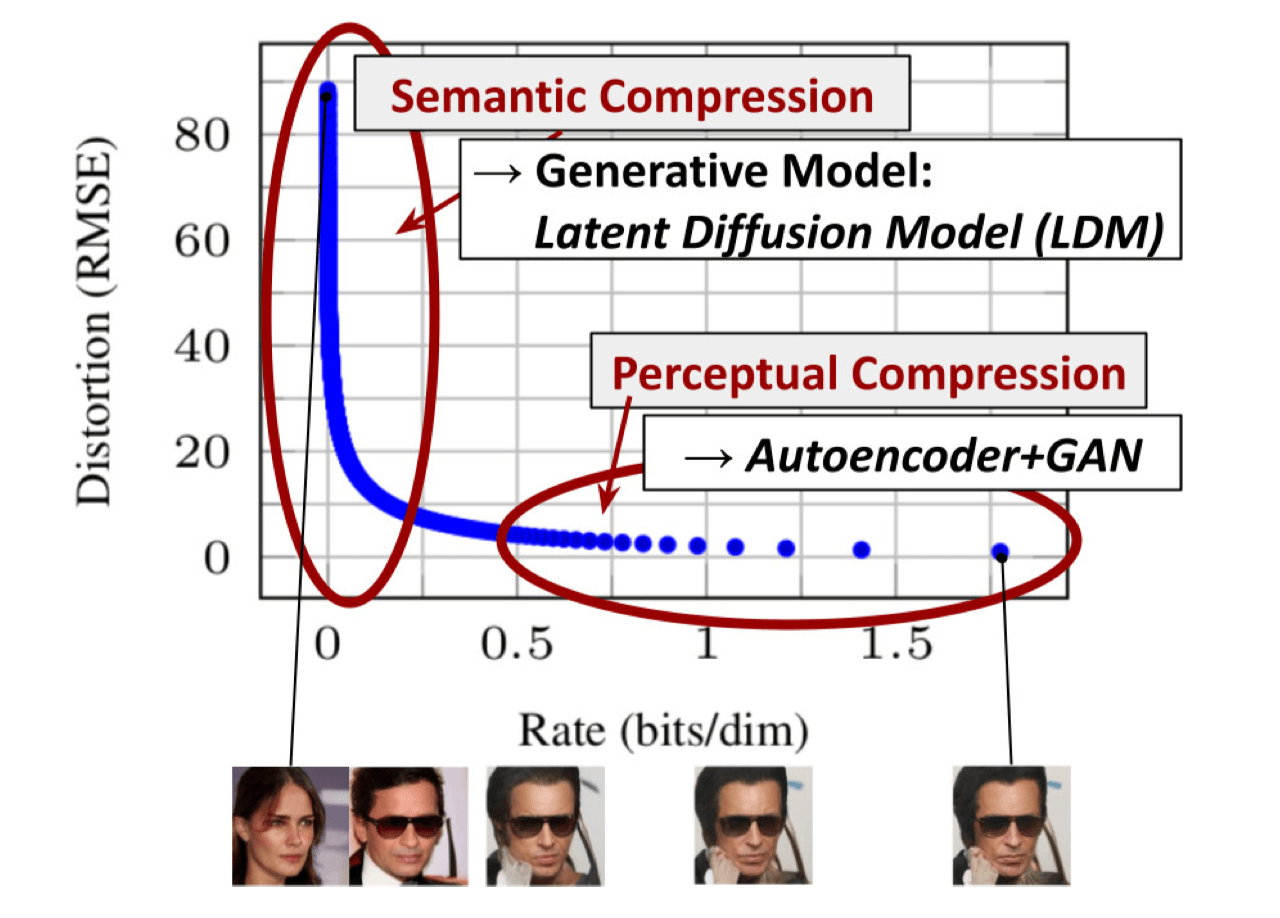
上图横轴是隐变量每个维度压缩的bit率,纵轴是模型的失真率。模型在学习的过程中,随着压缩率变大,刚开始模型的损失下降很快,后面下降很慢,但仍然在优化。模型首先学习到的是sematic(语义)部分的压缩/转换,然后学习到的是perceptual(细节)部分的压缩/转换。
Latent diffusion的网络结构
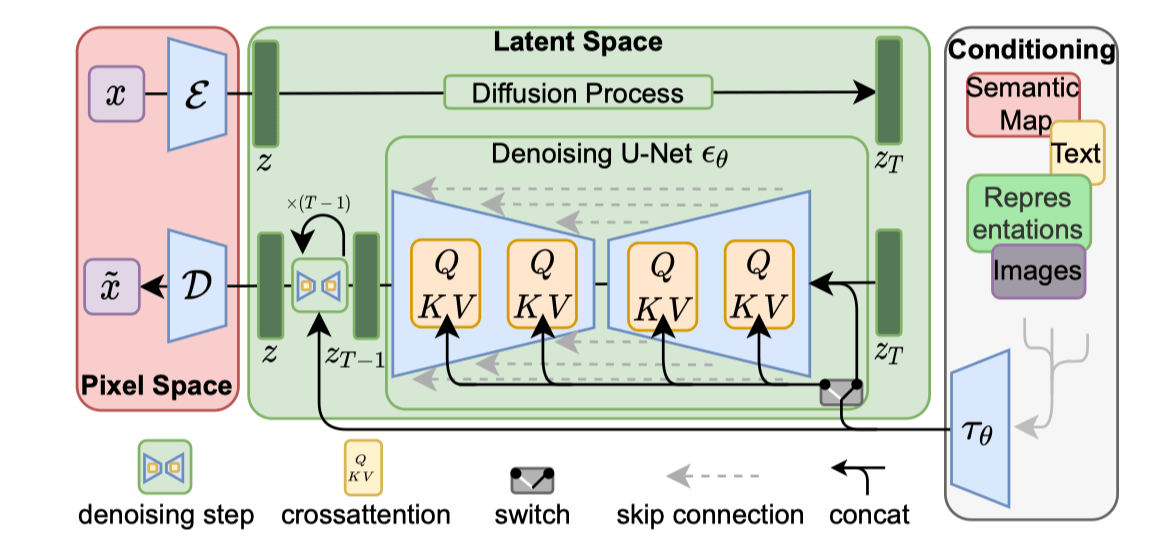
上图中,LDM网络分成三个主要分布,分别是 VAE的 Pixel Space, Diffusion的Latent Space以及条件输入部分(文本/图像输入)
Loss:
$L_{D M}=\mathbb{E}{x, \epsilon \sim \mathcal{N}(0,1),t}\left[\left|\epsilon-\epsilon_{\theta}\left(x_{t}, t\right)\right|_{2}^{2}\right]$
$L_{L D M}:=\mathbb{E}_{\mathcal{E}(x), \epsilon \sim \mathcal{N}(0,1), t}\left[\left|\epsilon-\epsilon_{\theta}\left({{\color{Red} z_{t}} } , t\right)\right|_{2}^{2}\right]$
$Attention (Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d}}\right) \cdot V ,$ .
with $Q=W_{Q}^{(i)} \cdot \varphi_{i}\left(z_{t}\right), K=W_{K}^{(i)} \cdot \tau_{\theta}(y), V=W_{V}^{(i)} \cdot \tau_{\theta}(y$)
$\varphi_{i}\left(z_{t}\right)\in \mathbb{R}^{N \times d_{\epsilon}^{i}}$: Unet $\epsilon_{\theta}$ 的中间表示。
$\tau_{\theta}(y) \in \mathbb{R}^{M \times d_{\tau}}$ : 将条件 $y$ 投影到中间表示。
$W_{V}^{(i)} \in \mathbb{R}^{d \times d_{\epsilon}^{i}}, W_{Q}^{(i)} \in \mathbb{R}^{d \times d_{\tau}} & W_{K}^{(i)} \in \mathbb{R}^{d \times d_{\tau}}$ 是可学习的投影矩阵。
->cross_attention
->q = self.to_q(x)
->k = self.to_k(context)
->v = self.to_v(context)
->sim = einsnum('b i d, b j d -> b i j', q, k)
->attn = sim.softmax(dim=1)
->out = einsum('b i j, b j d -> b i d', attn, v)
-> return nn.linear(out)
$L_{L D M}:=\mathbb{E}_{\mathcal{E}(x), y, \epsilon \sim \mathcal{N}(0,1), t}\left[\left|\epsilon-\epsilon{\theta}\left(z_{t}, t, \tau_{\theta}(y)\right)\right|_{2}^{2}\right]$
代码解析:
python scripts/txt2img.py --prompt "a photograph of an astronaut riding a horse" --plms
First Stage Model:
AutoencodeKL
encoder
self.encoder -> self.quant_conv -> DiagonalGaussianDistribution ?
get_learned_conditioning??
decoder
cond = model.get_learned_conditioning(prompts)
samples_ddim = plms.sample(...)
->plms_samping()
->get_model_output()
->apply_model()
->DiffusionWarpper(unet_config, conditioning_key)
->self.diffusion_model(x, t, c_crossattn)
->opeanimodel UNetMode(x, timestep=t, context=cc)
->self.inputblocks()
->cross_attention
->q = self.to_q(x)
->k = self.to_k(context)
->v = self.to_v(context)
->sim = einsnum('b i d, b j d -> b i j', q, k)
->attn = sim.softmax(dim=1)
->out = einsum('b i j, b j d -> b i d', attn, v)
->return nn.linear(out)
->self.middlle_block()
->self.output_blocks()
->
img = torch.randn(shape, device=device)
x_samples_ddim = model.decode_first_stage(samples_ddim)
一些参数
| ImageSize | 512x512 |
|---|---|
| Database | LAION-5B |
| TextEncoder | CLIP ViT-L/14 |
| UNet(diffusion) | 860M |